Weeks 11 & 12
Making Sisyphus Kinetic Art Table.
Team Griffin
This week we worked together in Team Griffin: Ondřej Plšek, Vojtěch Mareček, Filip Švadlenka, Jan Doležil, Lukáš Trčka, Nastasja Samochvalova, and Anna Svobodová. Our task was to build a computer-controlled machine (assignment details).
Sand Art Concept
We came up with the idea to draw relaxing patterns and images in sand.


Video Demonstrations
Here are a few videos showcasing the machine's quiet, soothing movements:
My Contribution
I wrote process_scara_gcode.py to convert designs from
Sandify directly into SCARA
motor commands.
import os
import sys
import math
def parse_gcode(file_path):
alpha = []
beta = []
with open(file_path, 'r') as f:
for line in f:
line = line.strip()
if line.startswith('G1') and 'X' in line and 'Y' in line:
parts = line.split()
x_val = None
y_val = None
for part in parts:
if part.startswith('X'):
try:
x_val = float(part[1:])
except ValueError:
pass
elif part.startswith('Y'):
try:
y_val = float(part[1:])
except ValueError:
pass
if x_val is not None:
alpha.append(x_val)
if y_val is not None:
beta.append(y_val)
return alpha, beta
def main():
# Absolute path to your .gcode file:
file_path = r'path\to\your\file\your_file_name.gcode'
if not os.path.isfile(file_path):
print(f"Error: file not found:\n {file_path}", file=sys.stderr)
sys.exit(1)
# parse the G-code file
raw_alpha, raw_beta = parse_gcode(file_path)
# number of decimal places
n = 3
# scaling factor k for angles in radians
k = - (1/6) * (2 * math.pi)
alpha_absolute = [round(x * k, n) for x in raw_alpha]
beta_absolute = [round(y * k, n) for y in raw_beta]
# total number of steps
n_steps = len(alpha_absolute)
# rotate to always start at home position
angle = alpha_absolute[0]
alpha_absolute = [round(x - angle, n) for x in alpha_absolute]
beta_absolute = [round(y - angle, n) for y in beta_absolute]
# convert to differences
alpha_relative = [alpha_absolute[0]] + [
round(alpha_absolute[i] - alpha_absolute[i-1], n)
for i in range(1, n_steps)
]
beta_relative = [beta_absolute[0]] + [
round(beta_absolute[i] - beta_absolute[i-1], n)
for i in range(1, n_steps)
]
# end difference from home position
home_alpha = -alpha_absolute[n_steps-1]
home_beta = -beta_absolute[n_steps-1]
# compute cartesian coordinates of all points in unit circle
midpoints = [
(
math.cos(math.pi/2 + a) * 0.5,
math.sin(math.pi/2 + a) * 0.5
)
for a in alpha_absolute
]
points = []
for (x1, y1), b in zip(midpoints, beta_absolute):
angle2 = math.pi/2 + b
x2 = x1 + math.cos(angle2) * 0.5
y2 = y1 + math.sin(angle2) * 0.5
points.append((x2, y2))
# scaling factor k for absolute motor rotation
k = 1 / (2 * math.pi) * (200 * 16) * (120 / 20)
alpha_motor_absolute = [round(x * k, n) for x in alpha_absolute]
beta_motor_absolute = [round(y * k, n) for y in beta_absolute]
# belt drift correction
correction = 1 / 1
beta_motor_absolute = [round(beta_motor_absolute[i] * correction, n) for i in range(n_steps)]
# convert to differences
alpha_motor_relative = [alpha_motor_absolute[0]] + [
round(alpha_motor_absolute[i] - alpha_motor_absolute[i-1], n)
for i in range(1, n_steps)
]
beta_motor_relative = [beta_motor_absolute[0]] + [
round(beta_motor_absolute[i] - beta_motor_absolute[i-1], n)
for i in range(1, n_steps)
]
# downsample to take every nth step
downsample = 3
alpha_motor_relative = alpha_motor_relative[::downsample]
beta_motor_relative = beta_motor_relative[::downsample]
# end difference from home position
modulo_base = round((200 * 16) * (120 / 20)) # equals 19200
home_alpha_motor = (-alpha_motor_absolute[n_steps - 1]) % modulo_base
home_beta_motor = (-beta_motor_absolute[n_steps - 1]) % modulo_base
if __name__ == "__main__":
main()
Design Experiments
At first we didn’t even use the SCARA robot. We tried a rotating arm with a carriage – selecting an angle and a radius. I made a prototype in Desmos.
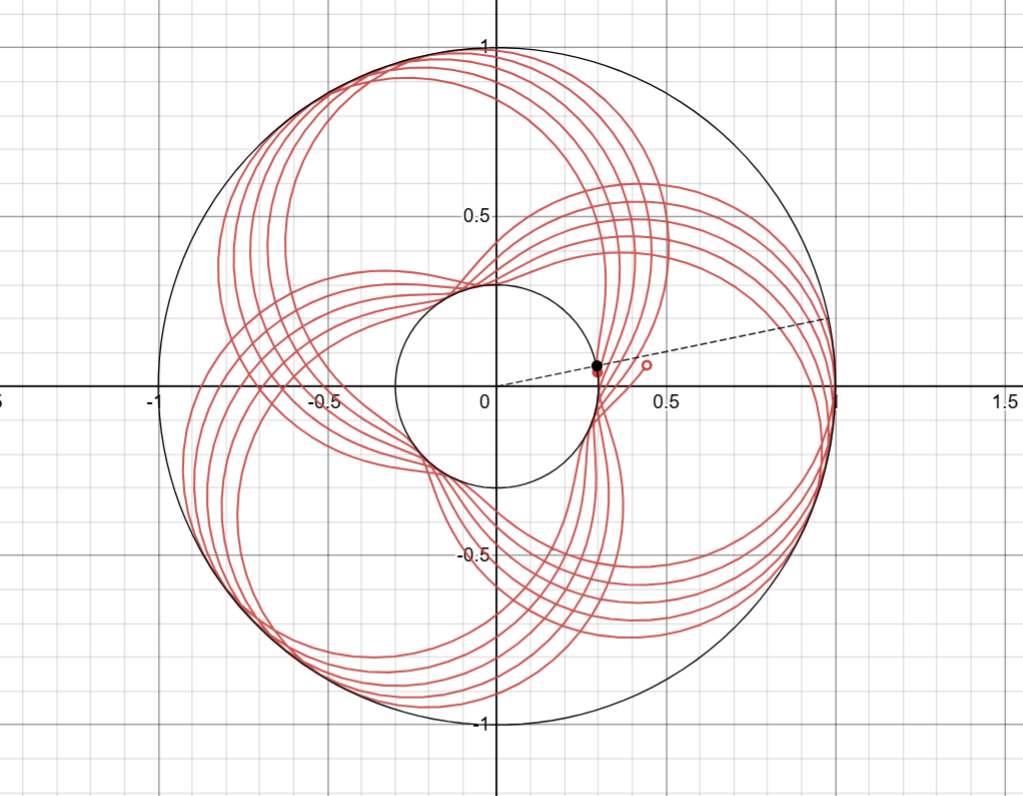
In the end we went for the SCARA robot – effectively choosing two angles for two arms. Not knowing how to draw a predetermined image, we set constant rotations on both arms and visualized the resulting pattern in a web app, since that makes endless zen patterns possible. I made another prototype in Desmos.
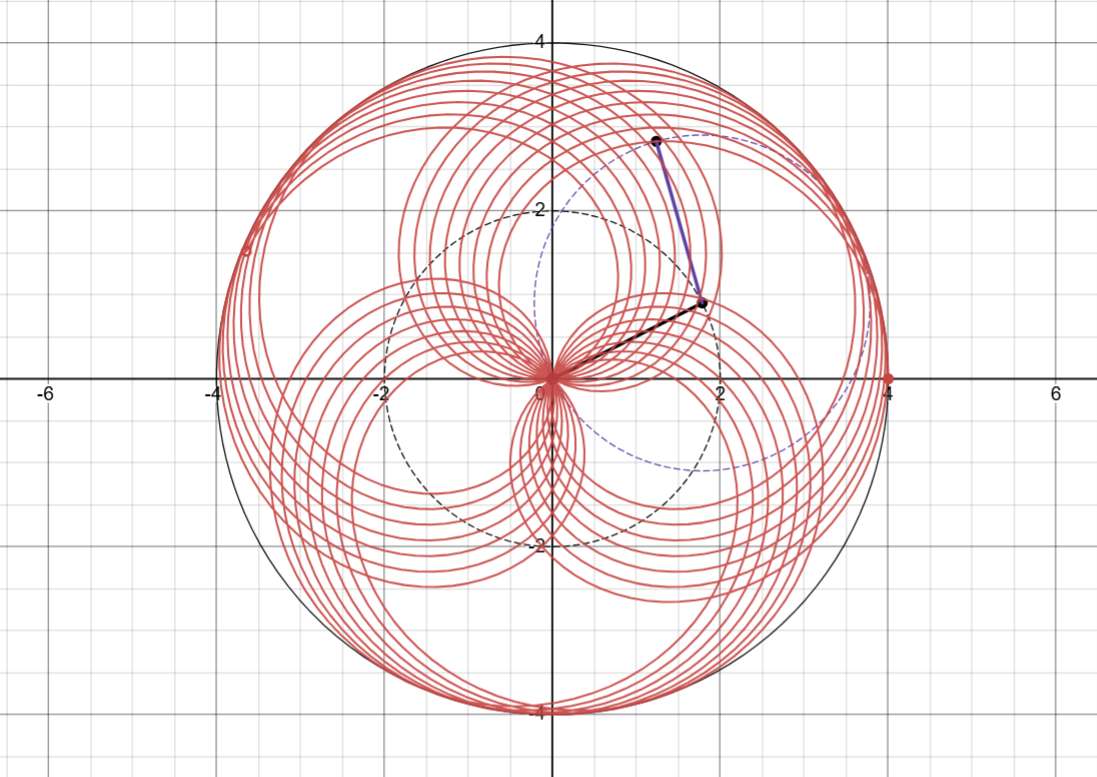
After conducting research, I refined the script and successfully demonstrated its correct operation with a dove pattern in Desmos.
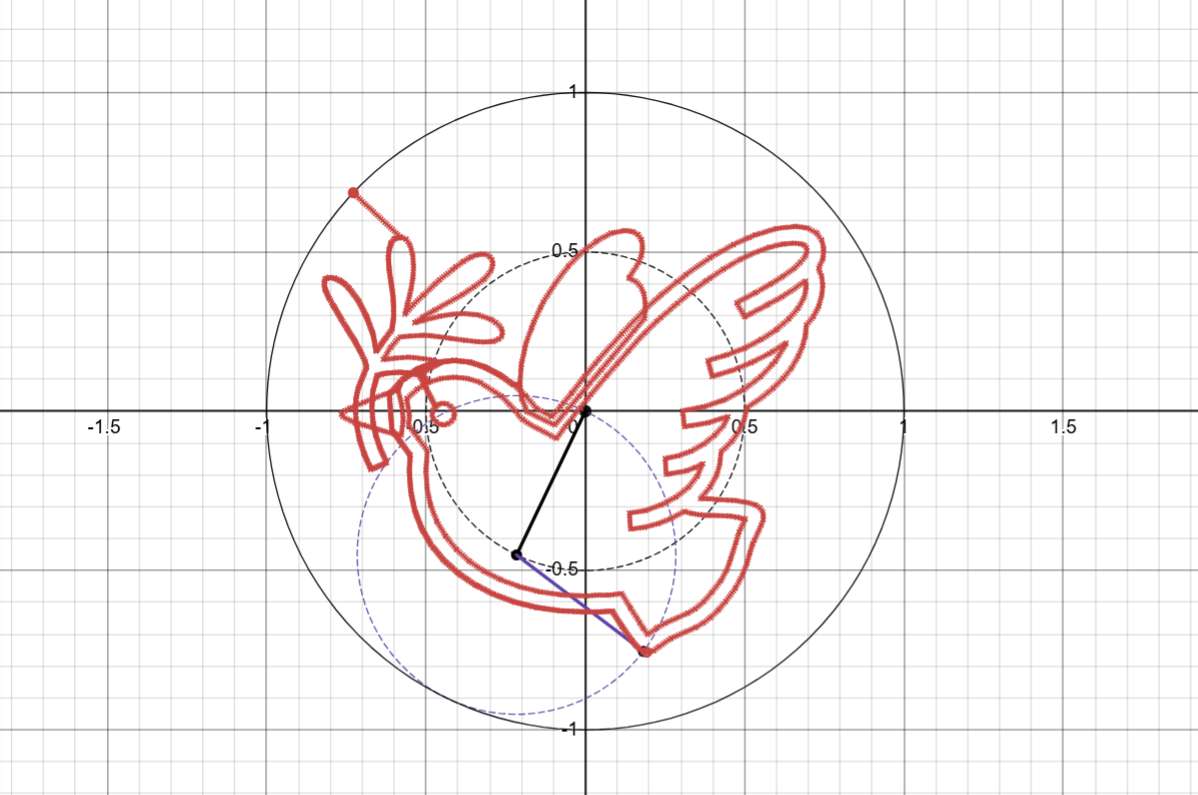
Soon, as the drawings became more complex, Desmos started to lag, so I wrote a new visualization script in Python. Here it is rendering a beautiful face:
Additional Work & Presentation
I also created a library of patterns for users to choose from. For full documentation, see our team site.
During presentations I saw other great projects, like this robotic croupier:
